以一道復習題為例淺談讓學生通過數學學會思維

瀘縣梁才學校 夏毅 熊曉蓉

鄭毓信教授是我尊敬并喜歡的一名教授，從2009年認識他，在這幾年中我都在向他學習著。他在他的《數學教育新論：走向專業成長》等幾本著作中，都談到了：“教師的教學活動，不要僅僅停留于‘幫助學生學會數學地思維’，應更加強調‘通過數學幫助學生學會思維’。是的，數學思維有其優點，也有其不足之處，作為數學教師，應該把眼光看長遠點，不應該只把思想限制在數學，應該從更廣闊的背景思考問題，這樣才能讓孩子的發展更趨優化與適宜。心理學上說的思維品質，實質是人的思維的個性特征，反映了每個個體智力或思維水平的差異。作為數學教學，要讓學生通過數學學習，證學生的思維品質得到個性化的發展，才是真正為孩子終身發展奠基。下面就以西師版二年級下冊數學109頁總復習第23題為例，談談通過數學學會思維。“P₁₀₆ 23. 把54只鴿子放養在籠子里，每個大籠放養9只，每個小籠放養6只，可以怎樣放？”這題的常規思路是：

方法1：只放大籠子：54÷9＝6（個）答：可以放6個大籠子。

方法2：只放小籠子：54÷6＝9（個）答：可以放9個小籠子。

方法3：兩種都放：(1)9×2＝18（只）6×6＝36（只）18+36=54(只)

(2)9×4＝36（只）6×3＝18（只）36+18=54(只)

答：可以放2個大籠子、6個小籠子；或者4個大籠子、3個小籠子。

但，這只是停留在一般計算上，思維訓練還不夠到位，現根據我的實踐，作這樣的疏理，目的是讓學生通過數學學會思維：

1. 思維的邏輯性與系統性。

對于解決問題，孩子們的難點是不能整體把握題意，條件之間的邏輯聯系少，讀了題之后，在頭腦中不能形成一個系統，條件、問題之間是支離破碎的，特別是條件多了之后，往往讀了后邊就忘了前面，他們不能用數學語言把條件概念化、不能用自己的話復述題意。怎樣培養學生思維的邏輯性與系統性，對這類題，教師不能認為很簡單，停留在是否列式正確了而一跑而過。應該從學生的語言規范性表達到簡潔性表達入手培養學生的思維的邏輯性與系統性。

這道題，到了期末，就題來說，應該大部分孩子都會做，但我們不能止步于此，否則對學生思維沒有質的提高?？梢赃@樣操作，學生初步了解題意后，可以用“如果……，那么……”關聯詞作為語句聯結，增加學生邏輯表達能力。這道題其實有三層意思：第一，如果每個大籠放養9只，那么要幾個籠子？第二，如果每個小籠放養6只，要幾個籠子？第三，如果既要大籠又要小籠，那么要幾個籠子？通過以上三句比較長的話的表達，可以訓練學生的思維以語言的形式顯性地表達出來。之后，再進一步，可以訓練學生的語言表達的簡潔、凝練，讓邏輯思維更強。即：三層意思分別是：第一，只放養大籠；第二，只放放養小籠；第三，兩種籠子都要。從實踐來看，學生更喜歡簡潔表達，這就從語言訓練進入到了思維的簡潔上來了，讓三種情況以一個整體的、系統的方式呈現在學生腦海中，清晰可見。

2. 思維的靈活性與敏捷性。

學生對解決問題時思維的靈活性與敏捷性建立對計算的無障礙上。本題中，前提要使學生對乘法口訣與兩位數的加減法比較熟練，這樣對培養思維的靈活性與敏捷性才會事半功倍，如果孩子計算不能自動化、那么它就會成為思維的障礙。通過前面對題的熟悉，孩子們應該能列出像54÷9＝，54÷6＝這樣的算式了，教學時，不要止步于只會列出算式，比如，我班的學生就會發現，兩個算式正好“反過來”，也就是除數與商變換了位置，孩子心目中的“反過來”正是“逆向思維”“思維的靈活性與敏捷性”的體現，他不只停留在某一個算式上，而關注到了算式之間的聯系。再通過兩種籠子都要的計算時，又有孩子發現“每當少一個大籠子，不能多出的鴿子，用小籠不能正好裝滿”，要“少兩個大籠子，多出的鴿子，才能剛好又多拿一個小籠了來裝”。然后教師列出相關的聯系式：

2個大籠 相當于 ( 3 )個小籠

4個大籠 相當于 ( 6 )個小籠

6個大籠 相當于 ( 9 )個小籠

發現算式問題之間的聯系，比做問題本身現重要，對于孩子思維遙靈活性與敏捷的培訓，不能只停留在事情本身上，要透過現象看本質，才能讓孩子的思維得到真正發展，否則，只能是以機械性的強化造成模式化的呆板。

3. 思維的廣闊性與深刻性。

小學階段，特別是才一二年級，因為孩子掌握知識比較少，往往給教者造成呆板的教學方式，以教科書的知識為準繩，一步都不能逾越，長期下去，就會讓孩子形成思維的定勢，無法達到思維的廣闊與深刻。

本題中，我們會遇到有余數的情況，而小學教材里，明確寫著“余數必須小于除數”，其實，這條準則，也多少限制了孩子的思維。我們可以變一種方式，讓學生思維能更廣闊、更深刻一點。

以“每個大籠放9只”為例列豎式如下：

從以上豎式，我們沒有把余數限定在必須比除數小這個命題上，而是按照實際分的過程來理解、來觀察。從以上的余數“45、36、27、18、9、0”中可以看出，剩下的鴿子只數哪些可以放在小籠子里而沒有剩余。通過6的乘法口訣，學生直觀看出余數是“36、18”兩種情況可以用小籠子裝而沒有剩余。而更重要的是這種思維方式，讓學生更深刻理解了分的過程，而不是枯燥地記住“余數必須比除數小”這樣的結論。并且，在生活中，也有這樣的原型，如，媽媽拿一包糖出來分給幾個人，并不是說一次性地就要把一包糖全部分完，而大多數是只分其中一部分。而這時的余數，往往剩很多，比除數大了好多。

4. 思維的獨創性與批判性。

作為新課程改革的核心而言，在數學教學，更重要的要培養孩子們的創造性思維。在本題中，我班孩子就提出了“可不可以大小兩個籠子套裝在一起”。我一聽，太好了，這是對常規的反叛、對傳統的挑戰。這正是我們教學中要追求的。孩子畫出了這樣的圖。這樣，大小籠子都是6個了。

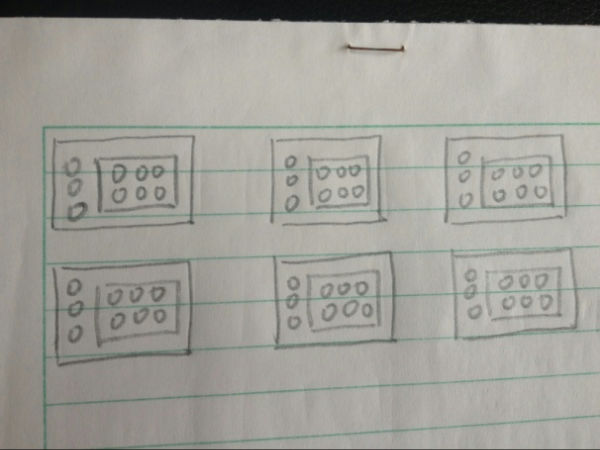
也有的孩子提出了，是不是必須要把每個籠子裝滿的問題，最后剩下的一個，可不可以不裝滿。總之，從孩子的表現中，可以看出他們是投入到了學習中去了的，他們的思維已經與數學聯系在一起了，并且通過數學在逐漸學會怎么思考問題了。